Day 3: Metrics

Yesterday we investigated the effect of using the 200-day simple moving average (200SMA) as a proxy for a rules-based investing method. The idea was to approximate what a reasonably rational actor/agent might do in addition to the buy-and-hold approach. When folks talk about research, backtesting, and forecast comparisons, they usually use a naive model against which one compares performance. In econometric forecasting, that naive approach is often represented mathematically as \(f(x_n) = x_{n-1}\) or something like that. Essentially, what you forecast tomorrow is what you observed today.

The investing equivalent of this is if you were long today, then you’re long tomorrow, or buy-and-hold. Actually being able to follow the naive approach is fraught with all the sorts of biases revealed and explored by the great duo, Kahneman and Tversky.¹ So, a more realistic approach is assuming some sort of rules-based investing. That too can become turtles all the way down if one questions whether most people have the behavioral discipline to follow a rules-based approach. Alternatively, we could use some sort of random trading as another benchmark, and we might just do that. But we don’t want too many comparisons; otherwise, our own feeble brains won’t be able to hold it all in.

Where do we stand? We have buy-and-hold, 60-40/50-50 with and without rebalancing, 200SMA, and 60-40/50-50 with 200SMA and with and without rebalancing. Already feels like too much. Let’s whittle it down to buy-and-hold, 200SMA, and 60-40 with rebalancing. By the way, the rebalancing happens every quarter at quarter end. While that’s fairly typical for many funds, it is also arbitrary from a fundamentally driven perspective. We won’t say more here, but will likely examine it in the future.

We’ve established the benchmarks, what about the metrics? We have return calculations like cumulative return, average return, and compound annual growth rate (CAGR), which are pretty standard. There are various measures of risk like volatility, Value-at-risk, \(\beta\), max drawdown, or win rate. There is a whole sea of risk-adjusted return ratios – e.g., the Sharpe, Treynor, Information, and/or Optimus.² Hybrid risk/efficiency metrics like Sortino, Calmar, and Omega. Rolling metrics like rolling \(\beta\), rolling Sharpe, rolling down the hill.

Choosing which metric or set of metrics is as much a matter of analytical rigor as it is of taste. And sometimes there’s no accounting for either. Cumulative return, the Sharpe Ratio, and max drawdown are pretty standard and seem to capture a lot of what one would want to measure. So we’ll go with those. Win rate is another common metric, which we’ll use too, but will save the discussion for another post.³ We also like seeing a rolling beta, or \(\beta\), graph, but it is not really relevant since asset selection is not important in this context. In which case, we’ll plot the rolling information ratio. Below we show the SPY 200SMA strategy against the 60-40 portfolio in a handy tear sheet format. We’ll discuss this in more detail tomorrow.

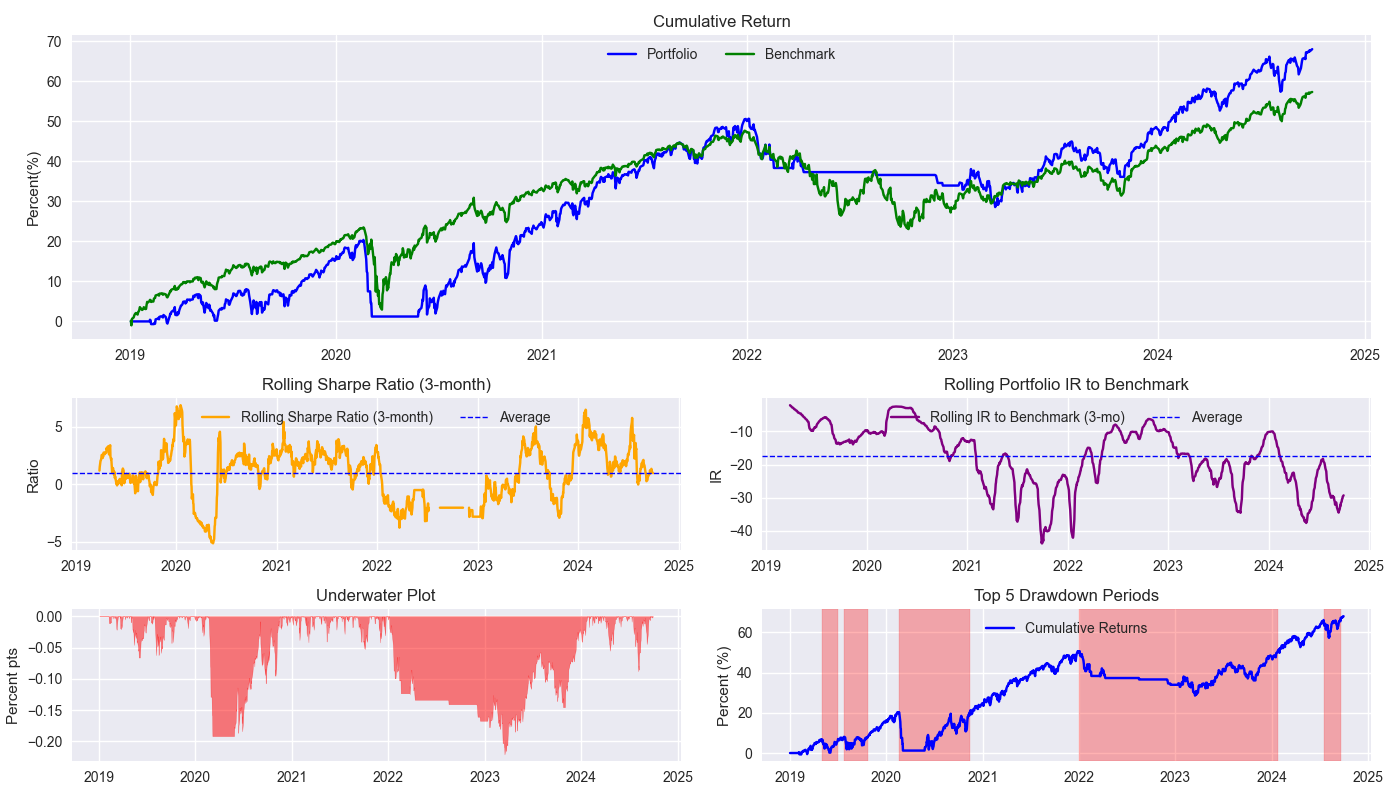
# Built using Python 3.10.19 and a virtual environment 


# Built using Python 3.10.19 and a virtual environment 

# Load packages
import pandas as pd
import numpy as np
import yfinance as yf
from datetime import datetime, timedelta
import statsmodels.api as sm
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec

plt.style.use('seaborn-v0_8')
plt.rcParams['figure.figsize'] = (14,8)


# Load Data
data = yf.download(['SPY', 'IEF'], start='2000-01-01', end='2024-10-01')
data.head()

# Clean up
df = data.loc["2003-01-01":, 'Adj Close']
df.columns.name = None
tickers = ['ief', 'spy']
df.index.name = 'date'
df.columns = tickers

# Add features
df[['ief_chg', 'spy_chg']] = df[['ief','spy']].apply(lambda x: np.log(x/x.shift(1)))
df[['ief_200sma', 'spy_200sma']] = df[['ief','spy']].rolling(200).mean()

for ticker in tickers:
    df[f"{ticker}_signal"] = np.where(df[ticker] > df[f"{ticker}_200sma"], 1 , 0)
    df[f"{ticker}_strat"] = df[f"{ticker}_chg"]*df[f"{ticker}_signal"].shift(1)

# Create functions for metrics and tearsheet
def calculate_portfolio_performance(weights: list, returns: pd.DataFrame, rebalance=False, frequency='month') -> pd.Series:
    # Initialize the portfolio value to 0.0
    portfolio_value = 0.0
    portfolio_values = []

    # Initialize the current weights
    current_weights = np.array(weights)

    # Create a dictionary to map frequency to the appropriate offset property
    frequency_map = {
        'week': 'week',
        'month': 'month',
        'quarter': 'quarter'
    }

    if rebalance:
        # Iterate over each row in the returns DataFrame
        for date, daily_returns in returns.iterrows():
            # Apply the current weights to the daily returns
            portfolio_value = np.dot(current_weights, daily_returns)
            portfolio_values.append(portfolio_value)

            # Rebalance at the selected frequency (week, month, quarter)
            offset = pd.DateOffset(days=1)
            next_date = date + offset

            # Dynamically get the attribute based on frequency
            current_period = getattr(date, frequency_map[frequency])
            next_period = getattr(next_date, frequency_map[frequency])

            if current_period != next_period:
                current_weights = np.array(weights)
            else:
                # Update weights based on the previous day's returns
                current_weights = current_weights * (1 + daily_returns)
                current_weights /= np.sum(current_weights)
    else:
        # No rebalancing, just apply the initial weights
        for date, daily_returns in returns.iterrows():
            portfolio_value = np.dot(current_weights, daily_returns)
            portfolio_values.append(portfolio_value)

            # Update weights based on the previous day's returns
            current_weights = current_weights * (1 + daily_returns)
            current_weights /= np.sum(current_weights)

    daily_returns = pd.Series(portfolio_values, index=returns.index)

    return daily_returns

def rolling_beta(portfolio_returns, market_returns, window=60, assume=True, threshold=2.0):
    def get_beta_coef(x_var, y_var):
        if assume:
            # coeffs = np.linalg.lstsq(x_var.values[:,np.newaxis], y_var)[0]
            coeffs = np.linalg.lstsq(np.vstack(x_var), y_var)[0]
            coeffs = coeffs if np.abs(coeffs) <= threshold else np.sign(coeffs)*threshold
            return coeffs[0]
        else:
            coeffs = np.linalg.lstsq(np.vstack([x_var, np.ones(len(x_var))]).T, y_var)[0]
            coeffs = coeffs if np.abs(coeffs) <= threshold else np.sign(coeffs)*threshold
            return coeffs[0]
    return portfolio_returns.rolling(window).apply(lambda x: get_beta_coef(x, market_returns.loc[x.index]))

# Rolling information ratio
def rolling_ir(portfolio_returns, market_returns, window=60):
    def get_tracking_error(portfolio, benchmark):
        return (portfolio - benchmark).std()
    return portfolio_returns.rolling(window).apply(lambda x: (x.mean() - market_returns.loc[x.index].mean())/get_tracking_error(x, market_returns.loc[x.index]))

# Define a function to calculate rolling Sharpe ratio
def rolling_sharpe_ratio(returns, window=60):
    rolling_sharpe = returns.rolling(window).mean() / returns.rolling(window).std() * np.sqrt(252)
    return rolling_sharpe

# Define a function to calculate drawdowns and identify drawdown periods
def get_drawdown_periods(cumulative_returns):
    peak = cumulative_returns.cummax()
    drawdown = cumulative_returns - peak

    end_of_dd = drawdown[drawdown == 0].index
    dd_periods = []
    start = cumulative_returns.index[0]
    for end in end_of_dd:
        if start < end:
            period = (start, end)
            dd_periods.append(period)
        start = end

    return drawdown, dd_periods
    
# Define a function to plot drawdowns
def plot_drawdowns(cumulative_returns):
    drawdown, dd_periods = get_drawdown_periods(cumulative_returns)
    dd_durations = [(end - start).days for start, end in dd_periods]
    top_dd_periods = sorted(dd_periods, key=lambda x: (x[1] - x[0]).days, reverse=True)[:5]
    return drawdown, top_dd_periods

# Make tearsheet function
def plot_tearsheet(portfolio_returns, market_returns, save_figure=False, title=None):
    cumulative_returns = portfolio_returns.cumsum()
    market_returns = market_returns.cumsum()

    fig = plt.figure(figsize=(14, 8))
    gs = GridSpec(3, 2, height_ratios=[2, 1, 1], width_ratios=[1, 1])

    # Cumulative return with no rebalancing plot
    ax0 = fig.add_subplot(gs[0, :])
    ax0.plot(cumulative_returns*100, label='Portfolio', color='blue')
    ax0.plot(market_returns*100, label='Benchmark', color='green')
    ax0.legend(loc='upper center', ncol=2)
    ax0.set_title('Cumulative Return')
    ax0.set_ylabel('Percent(%)')

    # Rolling Sharpe ratio (6-month) plot
    ax1 = fig.add_subplot(gs[1, 0])
    rolling_sr = rolling_sharpe_ratio(portfolio_returns)
    ax1.plot(rolling_sr, color='orange', label='Rolling Sharpe Ratio (3-month)')
    ax1.axhline(rolling_sr.mean(), color='blue', ls='--', lw=1, label='Average')
    ax1.legend(loc='upper center', ncol = 2)
    ax1.set_title('Rolling Sharpe Ratio (3-month)')
    ax1.set_ylabel('Ratio')

    # Rolling beta to SPY plot
    ax2 = fig.add_subplot(gs[1, 1])
    roll_ir = rolling_ir(portfolio_returns, market_returns)
    ax2.plot(roll_ir, color='purple', label='Rolling IR to Benchmark (3-mo)')
    ax2.axhline(roll_ir.mean(), color='blue', ls='--', lw=1, label='Average')
    ax2.legend(loc='upper center', ncol = 2)
    ax2.set_title('Rolling Portfolio IR to Benchmark')
    ax2.set_ylabel('IR')

    # Underwater plot
    ax3 = fig.add_subplot(gs[2, 0])
    drawdown, top_dd_periods = plot_drawdowns(cumulative_returns)
    ax3.fill_between(drawdown.index, drawdown, color='red', alpha=0.5)
    ax3.set_title('Underwater Plot')
    ax3.set_ylabel('Percent pts')

    # Top 5 drawdown periods plot
    ax4 = fig.add_subplot(gs[2, 1])
    for start, end in top_dd_periods:
        ax4.axvspan(start, end, color='red', alpha=0.3)
    ax4.plot(cumulative_returns*100, label='Cumulative Returns', color='blue')
    ax4.legend(loc='upper center')
    ax4.set_title('Top 5 Drawdown Periods')
    ax4.set_ylabel('Percent (%)')

    plt.tight_layout()
    if save_figure:
        fig.savefig(f'{title}.png')

    plt.show()

# Get return dataframes
bench_returns = df[['ief_chg', 'spy_chg']].copy()
bench_returns = bench_returns.loc['2019-01-01':]

strat_returns = df['spy_strat'].copy()
strat_returns = strat_returns.loc['2019-01-01':]

weights = [0.4,0.6]
bench_60_40_rebal = calculate_portfolio_performance(weights, bench_returns, rebalance=True, frequency='quarter')

# Plot tearsheet
plot_tearsheet(strat_returns, bench_60_40_rebal, save_figure=True, title="tearsheet_v0")