Day 9: Forecast

Yesterday we finished up our analysis of the regression models we built using different combinations of lookback and look forward momentum values. Today, we see if we can generate good forecasts using that data. If you’re wondering why we still haven’t tested Fibonacci retracements with Bollinger Band breakouts filtered by Chaikin Volatility, the reason is that we’re first trying to establish some rigor – albeit modest – to our tests. Can we find some combination of technical indicators that produce nice risk-adjusted returns in sample and not bad ones out-of-sample? Maybe. Will we know why that combination and not another worked? Doubtful. Will these combinations be based on a logical hypothesis on what drives asset returns? Doubtful again. There’s a good chance that if its successful it will be a narrative fit to results, as opposed to thesis borne out by the data.

Allocating capital based on trading signals is an implicit forecast, as Rob Carver argued in Systematic Trading. We believe we should establish a testable hypothesis that leads to trading signals as opposed to testing trading signals until we’ve p-hacked a result. That way, if or when the hypothesis is proved wrong, we can refine our logic and retest, as opposed to changing the Bollinger Band breakout to 1.273 standard deviations from 1.537 when the Fibonacci is 38.2% instead of 23.6% on triple witching Friday, but 14.71% (Fib 6 divided by Fib 9 if you start at 0).

Enough tongue-wagging, let’s get to the numbers! Only one of the combinations exhibited a reasonably significant positive relationship between the lookback and look forward momentum, the 12-by-12. The two other combinations – 3-by-3 and 3-by-9 – had large, absolute size effects and solid significance. However, those two exhibited a negative relationship between the lookback and look forward combination, so might be more appropriate for a mean reversion strategy.

How would we use that information to build forecasts? We want a model that can tell us that whether the market will be going up or down in some subsequent period with reasonably acceptable accuracy. Enter data science and machine learning with a twist. The principles of these complementary disciplines recommend forming train and test sets of the data in which, surprisingly, you train a model on one set and test that model’s forecasts on the other. That is a reasonable approach, but often struggles with time series data like stock prices. The reasons fill stacks of scholarly tomes and journal articles, which we can’t review here. Suffice it to say that the data generating process from \(x_{t-12}\) to the present may not be relevant for the next periods up to \(x_{t+12}\). The future doesn’t look like what it used to be.

This effect becomes particularly pronounced if you’re using a training set with months or years of data and then forecasting multiple periods ahead. If you’re in a stable macro regime, it might work, but then again it might not. That doesn’t mean we shouldn’t use lots of data;¹ rather, use lots of data in a way that can approximate what you might have experienced at the time. One of the best ways to do this is to use walk-forward analysis. That is, we successively build models and update them based only on the data we have at the time and iterate this process forward.

Such analysis looks something like the following. Train on 8 periods of data – this could months, days, hours, etc. – forecast on the next two periods, and then move one period ahead, adding that period to the prior 8 or dropping the last period. In reality, we could choose any length of train and test data, any step forward, and any dropout we like. None are a priori better than the other. There are ways to select one that might produce better results – using either time series analysis or machine learning – but we’ll save that analysis for later.

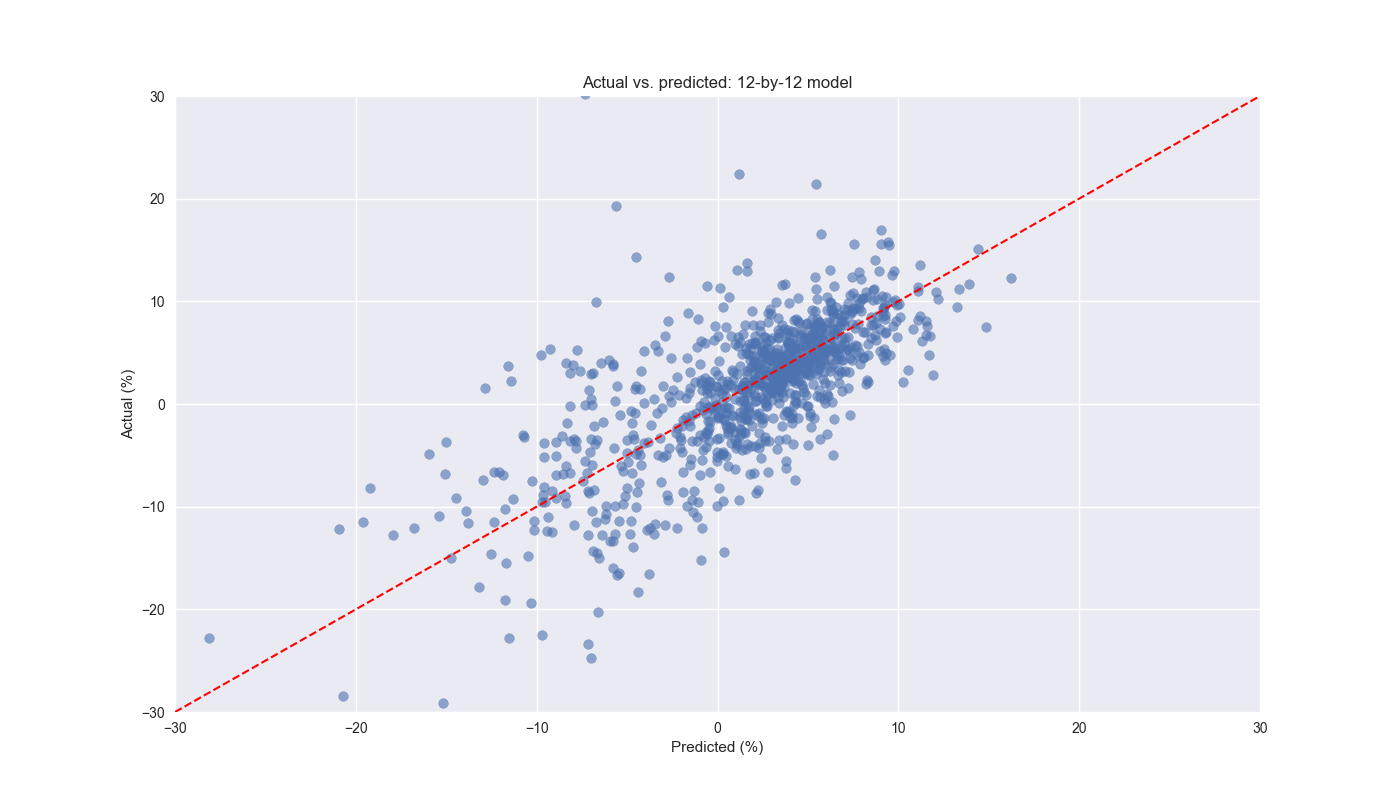
For now, we’ll just show a single step walk forward analysis on the 12-by-12 combination using 13 prior periods (roughly the number of weeks in a quarter) to train the model. Then we put the next period in the model to forecast the subsequent 12-week momentum. The graph below depicts the actual values vs. the predicted ones. We have limited the axes somewhat for ease of viewing, there are some outliers that are not shown. Nonetheless, the overall forecast looks pretty good from a clustering perspective. The red \(45^o\) line shows what a perfect model would look like. We’ll examine these results in more detail tomorrow. Code below.

# Built using Python 3.10.19 and a virtual environment 

# Load packages
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
import statsmodels.api as sm
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter
import yfinance as yf

plt.style.use('seaborn-v0_8')
plt.rcParams['figure.figsize'] = (14,8)

# Get data and clean
df = yf.download('SPY', start='2000-01-01', end='2024-10-01')
df.columns = ['open', 'high', 'low', 'close', 'adj close', 'volume']
df.index.name = 'date'

# Create training set and downsample to weekly ending Friday
df_train = df.loc[:'2019-01-01', 'adj close'].copy()
df_w = pd.DataFrame(df_train.resample('W-FRI').last())
df_w.columns = ['price'] 
df_w.head()

# Create lookback/look forward model combinations
periods = [3, 6, 9, 12]
momo_dict = {}
for back in periods:
    for forward in periods:
        df_out = df_w.copy()
        df_out['ret_back'] = np.log(df_out['price']/df_out['price'].shift(back))
        df_out['ret_for'] = np.log(df_out['price'].shift(-forward)/df_out['price'])
        df_out = df_out.dropna()

        mod = sm.OLS(df_out['ret_for'], sm.add_constant(df_out['ret_back'])).fit()
        momo_dict[f"{back} - {forward}"] = {'data': df_out,
                                            'params': mod.params,
                                            'pvalues': mod.pvalues}

# Conduct walk-forward analysis on 12-by-12
test = momo_dict['12 - 12']['data']

train_pd = 13
test_pd = 1
tot_pd = train_pd + test_pd

fcst_dict = {}
for i in range(tot_pd, len(test), test_pd):
    train_df = test.iloc[i-tot_pd:i-test_pd, 1:]
    test_df = test.iloc[i-test_pd:i, 1:]
    
    # Ensure 'ret_back' is 2D by selecting it as a DataFrame, not a Series
    X_train = sm.add_constant(train_df[['ret_back']])
    
    # If test_df has only one row adjust for statsmodels nuance
    if test_df.shape[0] > 1: 
        X_test = sm.add_constant(test_df[['ret_back']])
    else:
        X_test = sm.add_constant(test_df[['ret_back']], has_constant='add')

    # Fit the model
    mod_run = sm.OLS(train_df['ret_for'], X_train).fit()

    # Predict using the test data
    pred = mod_run.predict(X_test).values[0]

    # Calculate RMSE and average actual values
    rmse = np.sqrt(np.mean((pred - test_df['ret_for'].values) ** 2))
    actual = test_df['ret_for'].values[0]
    if test_df.shape[0] > 1:
        period = f"{str(test_df.index[0])[:10]} - {str(test_df.index[-1])[:10]}"
    else:
        period = f"{str(test_df.index[0])[:10]}"
    
    # Store forecast results
    fcst_dict[period] = {'rmse': rmse, 'actual': actual, 'predicted': pred}

# Convert dictionary to dataframe
df_fcst = pd.DataFrame(fcst_dict).T

# Plot predicted vs. actual
plt.figure()
plt.scatter(df_fcst['predicted']*100, df_fcst['actual']*100, alpha=0.6)
plt.plot([-30,30], [-30,30], 'r--', linewidth=1.5)
plt.xlim(-30,30)
plt.ylim(-30,30)
plt.xlabel("Predicted (%)")
plt.ylabel("Actual (%)")
plt.title('Actual vs. predicted: 12-by-12 model')
plt.show()