Day 14: Snooping

Guess what? The model we built in our last post actually suffers from snooping. We did this deliberately to show how easy it is to get mixed up when translating forecasting models into trading signals. Let’s explain. Our momentum model uses a 12-week cumulative return lookback to forecast the next 12-week cumulative return. That may have produced a pretty good explanatory model compared to the others. But we need to be careful. We train on a block of 5 12-week lookback cumulative returns. We then use the next 12-week cumulative return step to make a forecast. But our forecast is for the next 12-week cumulative return. So say we tried to implement this model. What model would we use to give us a trading signal? The one that was trained on data from twelve weeks ago!

Here’s an example. Say January 1 was the last date of the 5 block training period. The cumulative lookback return for that date would be for the period from October 9 to January 1 – 12 weeks. The period for the prior step (e.g., December 25, unlikely but this is just an example) would be October 2 to December 25 and so on. The target variable for January 1 would be the cumulative return from January 1 to March 25, the cumulative return for the December 25 timestamp would be December 25 to March 18 and so on. Since we won’t have the cumulative return for the period January 1 to March 25 until March 25, we can’t use that model until then.

Say we wanted to use that model to forecast returns. On March 25, we’d finally have the data to populate the forward returns associated with the January 1 block to be able to train the model. We’d, of course, have the lookback returns from January 8 that we would be using to forecast the forward returns to April 1. We’d also have cumulative lookback returns from January 8 to March 25, since they’ve already happened. This last fact, while important, won’t be addressed here.

If we don’t align our forecasts with when the data becomes available, we make a big error in prediction – snooping! That is, forecasting with data we wouldn’t have had in real time. We purposely did not align the data properly (which one can see in the code) in the last post and that is why the returns look great, but are not at all realizable. What can we do to fix this? Aligning the dates properly obviously! Another is to use the training model, but forecast with more up-to-date data and then move to a new model when we get new data. This still leaves us with using a model that was trained on data from weeks ago, which begs the question, do we want to make investment decisions on potentially stale data? That said, there’s always a trade-off around data recency. When you use the 200-day SMA, are the first 50, 100, or 150 days in the average contributing that much relevant information? A market maven will tell you they do only insofar as everyone else is looking at the 200-day. But how relevant older data is, remains an open question.

For the first fix, we could simply move the forecast up 12 steps from the end of initial training period. Why not 12 plus one more for the forecast step? We already have the data we’d use to forecast the next 12-week return, so we don’t have to wait another week.¹ In fact, if we did, we’d essentially be forecasting the past!² So, let’s see what this performance looks like.

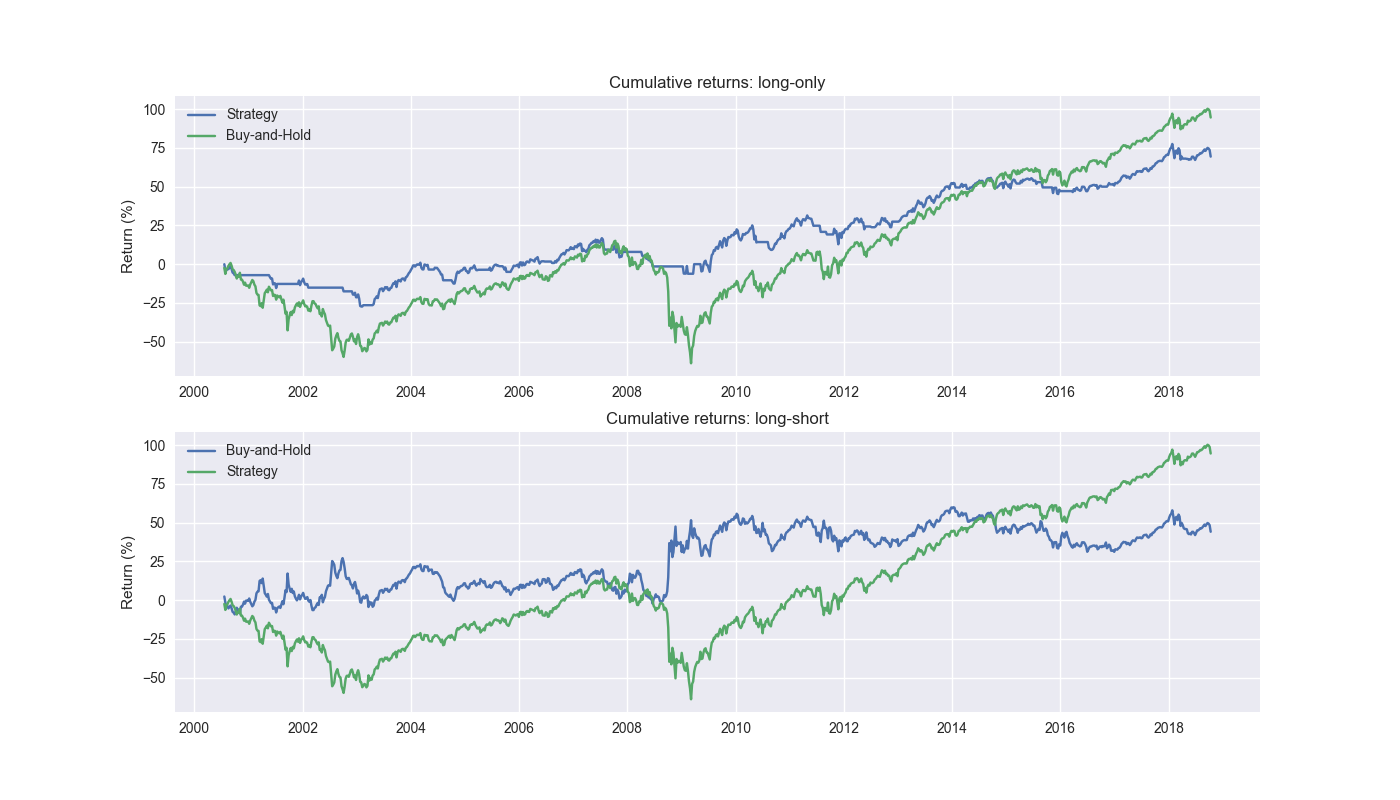
Not as good as the snooped model, as it underperforms buy-and-hold on a cumulative return basis. However, the Sharpe ratio is modestly better for the long-only strategy. The long-short strategy underperforms on both cumulative and risk-adjusted returns. Suffice it to say, not snooping does not perform very well! We’ll look at the other fixes tomorrow.

Code below.

# Built using Python 3.10.19 and a virtual environment 

# Load libraries
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
import statsmodels.api as sm
import matplotlib.pyplot as plt
import yfinance as yf

plt.style.use('seaborn-v0_8')
plt.rcParams['figure.figsize'] = (14,8)

# Function to get data
def get_spy_weekly_data() -> pd.DataFrame:
    df = yf.download('SPY', start='2000-01-01', end='2024-10-01')
    df.columns = ['open', 'high', 'low', 'close', 'adj close', 'volume']
    df.index.name = 'date'

    # Create training set and downsample to weekly ending Friday
    df_train = df.loc[:'2019-01-01', 'adj close'].copy()
    df_w = pd.DataFrame(df_train.resample('W-FRI').last())
    df_w.columns = ['price'] 

    return df_w

# Get data
df_w = get_spy_weekly_data()

# Create momentum dictionary
periods = [3, 6, 9, 12]
momo_dict = {}
for back in periods:
    for forward in periods:
        df_out = df_w.copy()
        df_out['ret_back'] = np.log(df_out['price']/df_out['price'].shift(back))
        df_out['ret_for'] = np.log(df_out['price'].shift(-forward)/df_out['price'])
        df_out = df_out.dropna()

        mod = sm.OLS(df_out['ret_for'], sm.add_constant(df_out['ret_back'])).fit()
        momo_dict[f"{back} - {forward}"] = {'data': df_out,
                                            'params': mod.params,
                                            'pvalues': mod.pvalues}

# Prepare model
model_name = '12 - 12'
mod_look_forward = 12
train_pd = 5
test_pd = 1
tot_pd = train_pd + test_pd

# Create trading dataframe
df_trade = momo_dict[model_name]['data'].copy()

# Run model with train/forecast steps
trade_pred = []
for i in range(tot_pd, len(df_trade)+1, test_pd):
    train_df = df_trade.iloc[i-tot_pd:i-test_pd, 1:]
    test_df = df_trade.iloc[i-test_pd:i, 1:]

    # Ensure 'ret_back' is 2D by selecting it as a DataFrame, not a Series
    X_train = sm.add_constant(train_df[['ret_back']])
    if test_df.shape[0] > 1:
        X_test = sm.add_constant(test_df[['ret_back']])
    else:
        X_test = sm.add_constant(test_df[['ret_back']], has_constant='add')

    # Fit the model
    mod_run = sm.OLS(train_df['ret_for'], X_train).fit()

    # Predict using the test data
    mod_pred = mod_run.predict(X_test).values
    trade_pred.extend(mod_pred)

# Add predictions to dataframe
# Snooped predictions. Pad = train_pd
# df_trade['pred'] = np.concatenate((np.repeat(np.nan,train_pd), np.array(trade_pred)))

# Non-snooped. Pad = mod_look_forward + train_pd 
df_trade['pred'] = np.concatenate((np.repeat(np.nan, mod_look_forward + train_pd - 1), np.array(trade_pred[:-(mod_look_forward - 1)])))

    
# Generate returns
df_trade['ret'] = np.log(df_trade['price']/df_trade['price'].shift(1))

# Generate signals
df_trade['signal'] = np.where(df_trade['pred'] == np.nan, np.nan, np.where(df_trade['pred'] > 0, 1, 0))
df_trade['signal_sh'] = np.where(df_trade['pred'] == np.nan, np.nan, np.where(df_trade['pred'] >= 0, 1, -1))

# Generate strategy returns
df_trade['strat_ret'] = df_trade['signal'].shift(1) * df_trade['ret']
df_trade['strat_ret_sh'] = df_trade['signal_sh'].shift(1) * df_trade['ret']

# Plot cumulative performance plot for long-only and long-shor
fig, (ax1, ax2) = plt.subplots(2,1)

top = df_trade[['strat_ret_snoop', 'ret']].cumsum()
bottom = df_trade[['strat_ret_snoop_sh', 'ret']].cumsum()

ax1.plot(top.index, top.values*100)
ax1.set_xlabel("")
ax1.set_ylabel("Return (%)")
ax1.legend(['Strategy', 'Buy-and-Hold'], loc="upper left")
ax1.set_title("Cumulative returns: long-only")

ax2.plot(bottom.index, bottom.values*100)
ax2.set_xlabel("")
ax2.set_ylabel("Return (%)")
ax2.legend(['Strategy', 'Buy-and-Hold'], loc="upper left")
ax2.set_title("Cumulative returns: long-short")

plt.show()