Day 23: Logic or Luck

On Day 22 we saw a meaningful improvement in our strategy by waiting an additional week to quantify model error and then using that error term to adjust the prediction on the most recently completed week of data. What was even more dramatic was comparing this improved strategy to one that followed the same waiting logic, but did not include the error correct. It turned an underperforming strategy into an outperforming one!

The corrected strategy outperforms buy-and-hold, the original strategy, and the unadjusted strategy by 20%, 10%, and over 50% points, respectively. Interestingly, it slightly underperforms the original strategy on a risk-adjusted basis with a Sharpe Ratio of 0.49 vs. 0.53 for the original strategy, which outperformed buy-and-hold by over 20% points. What’s going on here? Why would such a simple error correction yield such improved performance? Is there a logical reason or is it just luck? Can we prove it’s one or the other? Strap in because this is going to be a dense discussion that wouldn’t end with this post.

What we know about the error correction is this. In machine learning, many algorithms use a loss function to tweak a model’s parameters to minimize prediction error. This loss function is often the mean-squared error or the square of the residual, which is the actual value less the predicted value. These algorithms take the derivative of the loss function with respect to the predicted value to get the slope of the predicted value relative to the loss. This derivative can be used to tell the algorithm how much to adjust the prediction.¹ The adjustment is made by subtracting that error term multiplied by some factor (usually called the learning rate) from the old prediction. Why subtract? If the slope of tangent line is positive, that means the error increases with an increasing value of the prediction. In other words, the predictions are overshooting to the upside, so the algorithm should adjust in the opposite direction.

Here’s a good way to visualize this. Below we use one of the models generated in the 12-by-12 walk-forward algorithm and arbitrarily select a range of prediction values to plot the loss function. We then plot the derivatives of the loss function at different points to show that a line with a positive slope matches an increasing value of the loss function. Hence, the correction should be in the opposite direction to move toward the valley of the loss function. One should note that this adjustment is an iterative process that occurs in the training of the model somewhat like trial and error. The model we’re using is a linear regression, which generally doesn’t require such iteration and can be solved algebraically.²

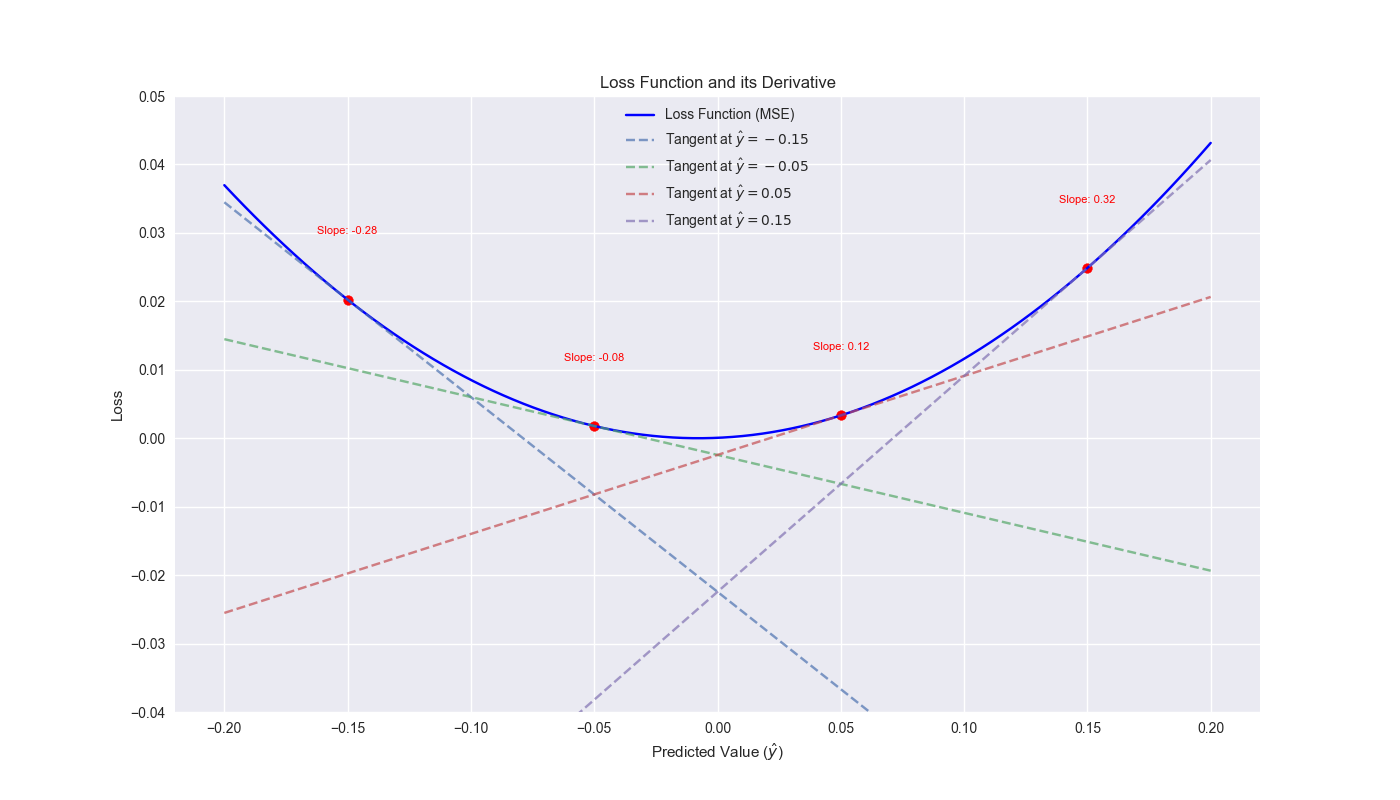
We used a similar loss function as in machine learning to adjust our model. But we experimented with different learning rates and added, not subtracted, the error term. What gives? We admit this was a hacky approach and may not seem intuitive or logical at all! The reason it worked out favorably is due to the correlation between the sign of the error term and the sign of the forward return as well as the effect of that error term on correlation between the sign of the prediction and the sign of the forward return.

That’s a pretty dense statement. Let’s parse it. Recall our trading signal: if the prediction is positive, go long; if negative, close or go short. Ideally, we’d like the sign of the prediction to be highly, positively correlated with sign of the return after we make the trade. In other words we want: \[\rho_{sign(pred_{t}), sign(ret_{t+1})} > 0\] Where \(\rho\) is the correlation coefficient, \(sign(pred_{t})\) is the sign of prediction that generates the trading signal (e.g., 1, 0, or -1 if shorting) at time \(t\) and \(sign(ret_{t+1})\) is the sign of the return in the next period, \(t + 1\), after one enters the trade. With the error correction the correlation is \[\rho_{sign(pred_{t} + error_{t-12}), sign(ret_{t+1})} > 0\] Note the error term is at \(t-12\), since it is based on the forecast for the 12-week forward return. In any case, for the error correction to have a positive impact on the performance, we want: \[\rho_{sign(pred_{t} + error_{t-12}), sign(ret_{t+1})} > \rho_{sign(pred_{t}), sign(ret_{t+1})}\] In other words, the sign of the error correction term added to the the prediction generates a higher correlation with the next period return than just the prediction on its own. This is in fact what happens.³ The effect of the error term likely the pushes the prediction into the correct direction sufficient to capture more the upward trend in the market while avoiding more down drafts.

We’ll stop here as this was a lot to digest. But we’ll leave the reader with one question. Have we answered the logic vs. luck question? Stay tuned for our next post.

Code below.

# Built using Python 3.10.19 and a virtual environment 

# Load packages
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
import statsmodels.api as sm
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter
from utils_intraday import *
import yfinance as yf
from tqdm import tqdm
import seaborn as sns
from scipy.stats import t
# from scipy.ndimage import gaussian_filter1d

plt.style.use('seaborn-v0_8')
plt.rcParams['figure.figsize'] = (14,8)

def get_spy_weekly_data() -> pd.DataFrame:
    df = yf.download('SPY', start='2000-01-01', end='2024-10-01')
    df.columns = ['open', 'high', 'low', 'close', 'adj close', 'volume']
    df.index.name = 'date'

    # Create training set and downsample to weekly ending Friday
    df_train = df.loc[:'2019-01-01', 'adj close'].copy()
    df_w = pd.DataFrame(df_train.resample('W-FRI').last())
    df_w.columns = ['price'] 

    return df_w

df_w = get_spy_weekly_data()

# Create momentum dictionary
periods = [3, 6, 9, 12]
momo_dict = {}
for back in periods:
    for forward in periods:
        df_out = df_w.copy()
        df_out['ret_back'] = np.log(df_out['price']/df_out['price'].shift(back))
        df_out['ret_for'] = np.log(df_out['price'].shift(-forward)/df_out['price'])
        df_out = df_out.dropna()

        mod = sm.OLS(df_out['ret_for'], sm.add_constant(df_out['ret_back'])).fit()
        momo_dict[f"{back} - {forward}"] = {'data': df_out,
                                            'params': mod.params,
                                            'pvalues': mod.pvalues}

# df_trade = momo_dict['12 - 12']['data'].copy()

# Trade with error handling
df_trade_1 = momo_dict['12 - 12']['data'].copy()

mod_look_forward = 12
train_pd = 5
test_pd = 1
tot_pd = train_pd + test_pd
lr = 2

trade_pred = []
trade_pred_un = []
trade_pred_old = []
for i in range(tot_pd, len(df_trade_1)-mod_look_forward+1, test_pd):
    train_df = df_trade_1.iloc[i-tot_pd:i-test_pd, 1:]
    valid_df = df_trade_1.iloc[i-test_pd:i, 1:]
    uncorr_df = df_trade_1.iloc[i-test_pd+mod_look_forward-1:i-test_pd+mod_look_forward, 1:]
    test_df = df_trade_1.iloc[i-test_pd+mod_look_forward:i-test_pd+mod_look_forward+1, 1:]

    # Ensure 'ret_back' is 2D by selecting it as a DataFrame, not a Series
    X_train = sm.add_constant(train_df[['ret_back']])
    if valid_df.shape[0] > 1:
        X_valid = sm.add_constant(valid_df[['ret_back']])
    else:
        X_valid = sm.add_constant(valid_df[['ret_back']], has_constant='add')

    if uncorr_df.shape[0] > 1:
        X_uncorr = sm.add_constant(uncorr_df[['ret_back']])
    else:
        X_uncorr = sm.add_constant(uncorr_df[['ret_back']], has_constant='add')

    if test_df.shape[0] > 1:
        X_test = sm.add_constant(test_df[['ret_back']])
    else:
        X_test = sm.add_constant(test_df[['ret_back']], has_constant='add')

    # Fit the model
    mod = sm.OLS(train_df['ret_for'], X_train).fit()

    # Predict using the test data
    pred = mod.predict(X_valid).values
    actual = valid_df['ret_for'].values
    gamma = -(actual - pred)*lr
    # gamma = -1 if np.sign(actual) + np.sign(pred) == 0 else 1
    pred_old = mod.predict(X_uncorr)
    trade_pred_old.extend(pred_old)

    mod_pred = mod.predict(X_test).values
    trade_pred_un.extend(mod_pred)
    trade_pred.extend(mod_pred + gamma)

assert len(trade_pred) + mod_look_forward + train_pd == len(df_trade_1)
assert len(trade_pred_un) + mod_look_forward + train_pd == len(df_trade_1)

df_trade_1['pred'] = np.concatenate((np.zeros(mod_look_forward + train_pd), np.array(trade_pred)))
df_trade_1['pred_un'] = np.concatenate((np.zeros(mod_look_forward + train_pd), np.array(trade_pred_un)))
df_trade_1['pred_old'] = np.concatenate((np.zeros(mod_look_forward + train_pd - 1), np.array(trade_pred_old), np.zeros(1)))
df_trade_1['ret'] = np.log(df_trade_1['price']/df_trade_1['price'].shift(1))

df_trade_1['signal'] = np.where(df_trade_1['pred'] > 0, 1, 0)
df_trade_1['signal_un'] = np.where(df_trade_1['pred_un'] > 0, 1, 0)
df_trade_1['signal_old'] = np.where(df_trade_1['pred_old'] > 0, 1, 0)
df_trade_1['signal_sh'] = np.where(df_trade_1['pred'] >= 0, 1, -1)

df_trade_1['strat_ret'] = df_trade_1['signal'].shift(1) * df_trade_1['ret']
df_trade_1['strat_ret_un'] = df_trade_1['signal_un'].shift(1) * df_trade_1['ret']
df_trade_1['strat_ret_old'] = df_trade_1['signal_old'].shift(1) * df_trade_1['ret']
df_trade_1['strat_ret_sh'] = df_trade_1['signal_sh'].shift(1) * df_trade_1['ret']


# Select single set of data to create model for loss function
df_test = momo_dict['12 - 12']['data'].copy()

mod_look_forward = 12
train_pd = 5
test_pd = 1
tot_pd = train_pd + test_pd
i = tot_pd

train_df = df_test.iloc[i-tot_pd:i-test_pd, 1:]
valid_df = df_test.iloc[i-test_pd:i, 1:]
test_df = df_test.iloc[i-test_pd+mod_look_forward:i-test_pd+mod_look_forward+1, 1:]

# Ensure 'ret_back' is 2D by selecting it as a DataFrame, not a Series
X_train = sm.add_constant(train_df[['ret_back']])
if valid_df.shape[0] > 1:
    X_valid = sm.add_constant(valid_df[['ret_back']])
else:
    X_valid = sm.add_constant(valid_df[['ret_back']], has_constant='add')

if test_df.shape[0] > 1:
    X_test = sm.add_constant(test_df[['ret_back']])
else:
    X_test = sm.add_constant(test_df[['ret_back']], has_constant='add')

# Fit the model
mod = sm.OLS(train_df['ret_for'], X_train).fit()

# Predict using the test data
pred = mod.predict(X_valid).values
actual = valid_df['ret_for'].values
gamma = -(actual - pred)*lr
mod_pred = mod.predict(X_test).values
print(mod_pred)

# Define the loss function
def mse_loss(y_true, y_pred):
    return (y_true - y_pred) ** 2

# Derivative of the loss function with respect to y_pred
def mse_loss_derivative(y_true, y_pred):
    return -2*(y_true - y_pred)

# Predicted values range
y_pred = np.linspace(-0.2, 0.2, 100)

# Compute loss and its derivative
loss = mse_loss(actual, y_pred)
loss_derivative = mse_loss_derivative(actual, y_pred)

# Plot the loss function
plt.figure()
plt.plot(y_pred, loss, label="Loss Function (MSE)", color="blue")
plt.title("Loss Function and its Derivative")
plt.xlabel("Predicted Value ($\hat{y}$)")
plt.ylabel("Loss")

# Annotate the slope at a few key points
sample_points = [-0.15, -0.05, 0.05, 0.15]
for point in sample_points:
    slope = mse_loss_derivative(actual, point)
    tangent_line = slope * (y_pred - point) + mse_loss(actual, point)
    plt.plot(y_pred, tangent_line, "--", label=f"Tangent at $\hat{{y}}={point}$", alpha=0.7)
    plt.scatter([point], [mse_loss(actual, point)], color="red")
    plt.text(point, mse_loss(actual, point)+0.01, f"Slope: {slope[0]:.2f}", horizontalalignment='center', verticalalignment='center', fontsize=8, color="red")

# Add legend
plt.legend(loc='upper center')
plt.ylim(-0.04, 0.05)
plt.show()