Day 24: Lucky Logic

On Day 23 we dove into the deep end to understand why the error correction we used worked as well as it did. We showed how traditional machine learning uses loss functions and then hypothesized how our use helped improve predictions through its effect on the correlation of the signs of the prediction with that of the forward return. We have to admit that our decision to use the error term in the way we did was a bit hacky so while it did generate improvements vial trial and error, one wouldn’t have necessarily thought to use it in the way we did. So does that qualify as logic or luck?

Since we were experimenting with loss functions, this would point to luck. Is there a logic that the luck reveals? Or maybe there’s a different way of thinking about the results. Let’s tease out what the prediction we’re using really entails. We have a prediction based on model that is based on data at least 13 weeks old. We use that model to predict the most recently completed forward return. We find the residual of that prediction (e.g., actual less predicted value) and take the derivative of the loss function with respect to the predicted value. We then take the most recent 12-week cumulative return as an input into the model and add the derivative of the loss function. This addition sees a substantial improvement in trading performance vs. not adding the loss derivative and sees a solid improvement vs. the original 12-by-12 model.

Recall our trading signal is based on the sign of the prediction (e.g., if positive go long, if zero or negative close, stay flat, or go short). That means that if the adjusted strategy performs better than the unadjusted strategy, the loss derivative is flipping the sign on some occasions to capture the out-of-sample direction better than the base model. This might have to do with the residual error. If the model is overshooting (predicted > actual), the residual error is negative, but its sign flips with the derivative. Adding an error to a prediction that was already overshooting would seem to accentuate that error, unless there’s some degree of directional reversal in the near term actual vs. the 12-week forecast.¹ That is, even if the model would have predicted a negative value (due to a prior positive value and mean reverting model), the error correction would have outweighed negative prediction, yielding a positive value instead. If the market is trending, that keeps the strategy long.

Indeed, the walk-forward models tend to have negative size effects. Without going off on a statistical test tangent, we could suppose most of the models are mean reverting. So while each model will tend to predict some sort of reversion once a baseline threshold is surpassed,² the near-term direction might still be trending (going in the opposite direction of the forecast). Thus adding the error correction keeps the trade going. Alternatively, not all models have negative size or positive baseline effects, so it could also be the case that in some circumstances the error term hurts rather than helps. Clear as mud!

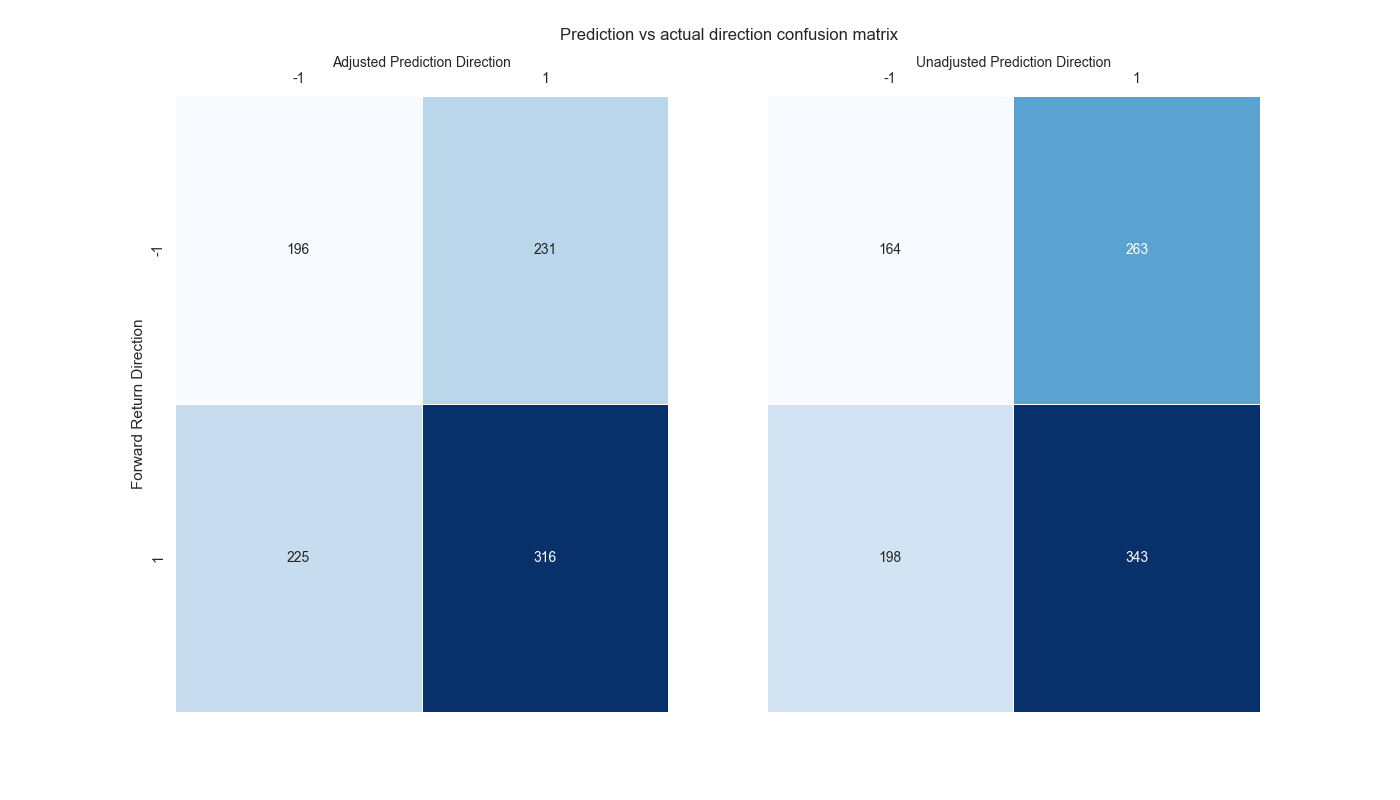
Whatever the case, the error correction is probably not going to get the near-term direction correct every time due to the inherent randomness of markets and that little \(\epsilon\) (random error) in the regression equation many of us ignore. How would we quantify how successful this error correction is? We can return to machine learning with some foundational confusion matrices. In the graph below, we show the different scenarios for when the predictions of the adjusted and unadjusted models match (both 1 or -1) or don’t match the direction of the underlying. We’ll have more to say on this in our next post. But for now, note that although the adjusted prediction has fewer instances of correctly predicting a positive direction than the unadjusted prediction (lower right box), it has more instances of correctly predicting the negative direction (upper left box). And the first rule of trading is don’t lose money! Code below.

# Built using Python 3.10.19 and a virtual environment 

# Load packages
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
import statsmodels.api as sm
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter
import yfinance as yf
import seaborn as sns

plt.style.use('seaborn-v0_8')
plt.rcParams['figure.figsize'] = (14,8)

def get_spy_weekly_data() -> pd.DataFrame:
    df = yf.download('SPY', start='2000-01-01', end='2024-10-01')
    df.columns = ['open', 'high', 'low', 'close', 'adj close', 'volume']
    df.index.name = 'date'

    # Create training set and downsample to weekly ending Friday
    df_train = df.loc[:'2019-01-01', 'adj close'].copy()
    df_w = pd.DataFrame(df_train.resample('W-FRI').last())
    df_w.columns = ['price'] 

    return df_w

df_w = get_spy_weekly_data()

# Create momentum dictionary
periods = [3, 6, 9, 12]
momo_dict = {}
for back in periods:
    for forward in periods:
        df_out = df_w.copy()
        df_out['ret_back'] = np.log(df_out['price']/df_out['price'].shift(back))
        df_out['ret_for'] = np.log(df_out['price'].shift(-forward)/df_out['price'])
        df_out = df_out.dropna()

        mod = sm.OLS(df_out['ret_for'], sm.add_constant(df_out['ret_back'])).fit()
        momo_dict[f"{back} - {forward}"] = {'data': df_out,
                                            'params': mod.params,
                                            'pvalues': mod.pvalues}

# df_trade = momo_dict['12 - 12']['data'].copy()

# Trade with error handling
df_trade_1 = momo_dict['12 - 12']['data'].copy()

mod_look_forward = 12
train_pd = 5
test_pd = 1
tot_pd = train_pd + test_pd
lr = 2

trade_pred = []
trade_pred_un = []
trade_pred_old = []
for i in range(tot_pd, len(df_trade_1)-mod_look_forward+1, test_pd):
    train_df = df_trade_1.iloc[i-tot_pd:i-test_pd, 1:]
    valid_df = df_trade_1.iloc[i-test_pd:i, 1:]
    uncorr_df = df_trade_1.iloc[i-test_pd+mod_look_forward-1:i-test_pd+mod_look_forward, 1:]
    test_df = df_trade_1.iloc[i-test_pd+mod_look_forward:i-test_pd+mod_look_forward+1, 1:]

    # Ensure 'ret_back' is 2D by selecting it as a DataFrame, not a Series
    X_train = sm.add_constant(train_df[['ret_back']])
    if valid_df.shape[0] > 1:
        X_valid = sm.add_constant(valid_df[['ret_back']])
    else:
        X_valid = sm.add_constant(valid_df[['ret_back']], has_constant='add')

    if uncorr_df.shape[0] > 1:
        X_uncorr = sm.add_constant(uncorr_df[['ret_back']])
    else:
        X_uncorr = sm.add_constant(uncorr_df[['ret_back']], has_constant='add')

    if test_df.shape[0] > 1:
        X_test = sm.add_constant(test_df[['ret_back']])
    else:
        X_test = sm.add_constant(test_df[['ret_back']], has_constant='add')

    # Fit the model
    mod = sm.OLS(train_df['ret_for'], X_train).fit()

    # Predict using the test data
    pred = mod.predict(X_valid).values
    actual = valid_df['ret_for'].values
    gamma = -(actual - pred)*lr
    # gamma = -1 if np.sign(actual) + np.sign(pred) == 0 else 1
    pred_old = mod.predict(X_uncorr)
    trade_pred_old.extend(pred_old)

    mod_pred = mod.predict(X_test).values
    trade_pred_un.extend(mod_pred)
    trade_pred.extend(mod_pred + gamma)

assert len(trade_pred) + mod_look_forward + train_pd == len(df_trade_1)
assert len(trade_pred_un) + mod_look_forward + train_pd == len(df_trade_1)

df_trade_1['pred'] = np.concatenate((np.zeros(mod_look_forward + train_pd), np.array(trade_pred)))
df_trade_1['pred_un'] = np.concatenate((np.zeros(mod_look_forward + train_pd), np.array(trade_pred_un)))
df_trade_1['pred_old'] = np.concatenate((np.zeros(mod_look_forward + train_pd - 1), np.array(trade_pred_old), np.zeros(1)))
df_trade_1['ret'] = np.log(df_trade_1['price']/df_trade_1['price'].shift(1))

df_trade_1['signal'] = np.where(df_trade_1['pred'] > 0, 1, 0)
df_trade_1['signal_un'] = np.where(df_trade_1['pred_un'] > 0, 1, 0)
df_trade_1['signal_old'] = np.where(df_trade_1['pred_old'] > 0, 1, 0)
df_trade_1['signal_sh'] = np.where(df_trade_1['pred'] >= 0, 1, -1)

df_trade_1['strat_ret'] = df_trade_1['signal'].shift(1) * df_trade_1['ret']
df_trade_1['strat_ret_un'] = df_trade_1['signal_un'].shift(1) * df_trade_1['ret']
df_trade_1['strat_ret_old'] = df_trade_1['signal_old'].shift(1) * df_trade_1['ret']
df_trade_1['strat_ret_sh'] = df_trade_1['signal_sh'].shift(1) * df_trade_1['ret']

df_trade_1['gamma'] = df_trade_1['pred'].sub(df_trade_1['pred_un'])

# Sign analysis
df_corr = df_trade_1[['pred', 'pred_un', 'pred_old', 'gamma', 'ret', 'ret_for', 'ret_back']].copy()

# Convert values to sign: -1 (negative), 0 (neutral), 1 (positive)
pred_sign = [1 if x == 1 else -1 for x in np.sign(df_corr['pred'])]
pred_un_sign = [1 if x == 1 else -1 for x in np.sign(df_corr['pred_un'])]
ret_sign = [1 if x == 1 else -1 for x in np.sign(df_corr['ret_lag'])]
pred_old_sign = [1 if x == 1 else -1 for x in np.sign(df_corr['pred_old'])]

# Create a DataFrame
pred_data = pd.DataFrame({'Prediction': pred_sign, 'Return': ret_sign})
pred_un_data = pd.DataFrame({'Prediction': pred_un_sign, 'Return': ret_sign})

# Create a heatmap of counts for each combination
pred_heatmap = pred_data.groupby(['Prediction', 'Return']).size().unstack(fill_value=0)

pred_un_heatmap = pred_un_data.groupby(['Prediction', 'Return']).size().unstack(fill_value=0)

# Annotations for confusion matrix
annot1 = pred_heatmap_percent.applymap(lambda x: f"{x:.1f}%").values
annot2 = pred_un_heatmap_percent.applymap(lambda x: f"{x:.1f}%").values
annot3 = pred_old_heatmap_percent.applymap(lambda x: f"{x:.1f}%").values

# Heatmap
fig, (ax1, ax2) = plt.subplots(1,2, sharey=True)
fig.text(0.4, 0.95, "Prediction vs actual direction confusion matrix", fontsize=12)

sns.heatmap(pred_heatmap, annot=True, fmt='d', cmap='Blues', cbar=False, linewidths=0.5, linecolor='white', ax=ax1)
ax1.xaxis.tick_top()
ax1.xaxis.set_label_position('top')  # Move the x-axis label to the top
ax1.set_xlabel('Adjusted Prediction Direction', fontsize = 10)
ax1.set_ylabel('Forward Return Direction')

sns.heatmap(pred_un_heatmap, annot=True, fmt='d', cmap='Blues', cbar=False, linewidths=0.5, linecolor='white', ax=ax2)
ax2.xaxis.tick_top()
ax2.xaxis.set_label_position('top')  # Move the x-axis label to the top
ax2.set_xlabel('Unadjusted Prediction Direction', fontsize = 10)
ax2.set_ylabel('')

plt.show()